Interpreting 4x 2 5x 12 0: Understanding Number Patterns
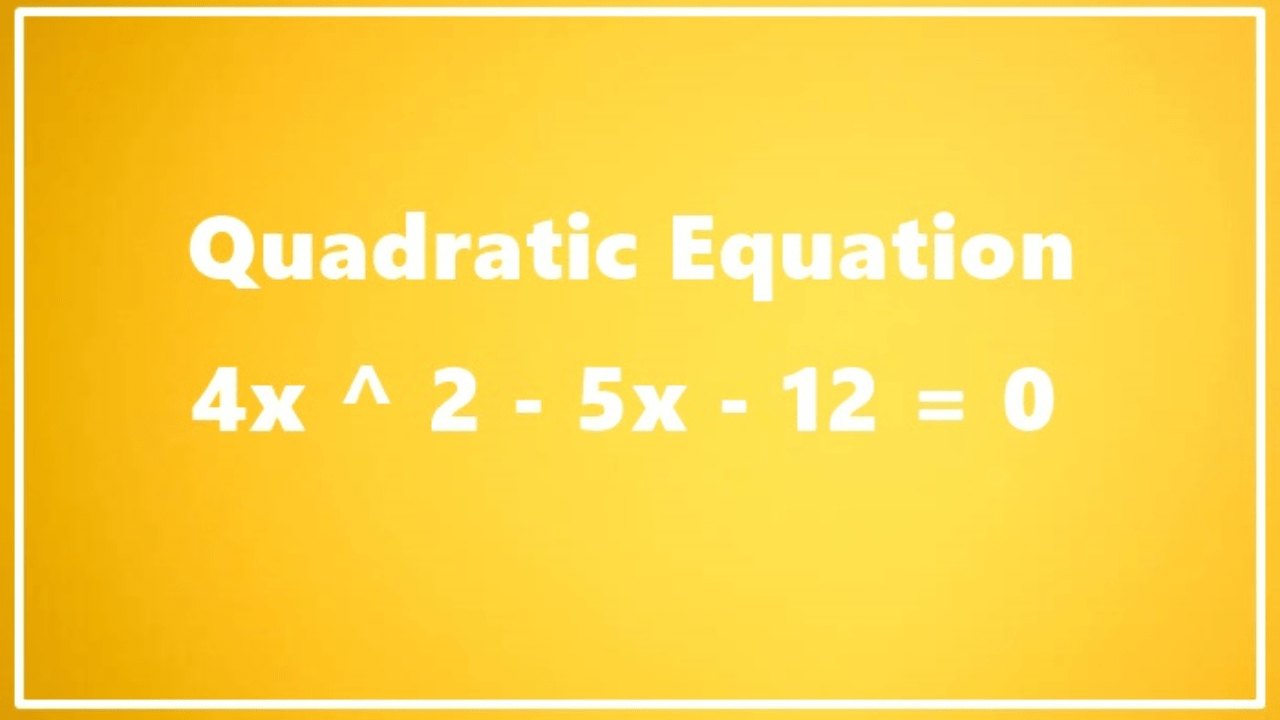
Understanding numerical sequences often unravels fascinating patterns and relations. The sequence 4x 2 5x 12 0 presents an intriguing set of numbers that, upon analysis, reveal underlying numerical structures and relationships.
Exploring the Sequence
At first glance, the sequence 4x 2 5x 12 0 may seem like a random arrangement of numbers and characters. However, closer inspection reveals a pattern worth exploring. Variables like x amidst numerical values hint at a mathematical expression or sequence that requires deciphering.
Identifying Patterns
The sequence suggests a mix of coefficients, constants, and the variable x, reminiscent of algebraic equations. The juxtaposition of these elements hints at a potential mathematical relationship waiting to be decoded. We can begin to discern patterns and possible equations that embody these numbers by analyzing the arrangement.
Unveiling Numerical Relations
Delving deeper into the sequence, we encounter alternating patterns between coefficients and constants. The repetitive appearance of x, coupled with numerical values, indicates a potential quadratic equation or a series of mathematical expressions.
Insights into Mathematical Structures
Upon meticulous examination, the sequence 4x 2 5x 12 0 could represent a quadratic equation as 4x² + 5x + 12 = 0. This interpretation aligns with the arrangement of terms and suggests a mathematical equation involving the variable x.
Exploring the Equation
The equation 4x² + 5x + 12 = 0 signifies a quadratic expression, where x represents an unknown value. Analyzing such equations often involves factoring, completing the square, or using the quadratic formula to determine potential solutions for x.
Diving Deeper into the Equation
The quadratic equation 4x² + 5x + 12 = 0 prompts a deeper examination of its roots or solutions for x. Quadratic equations typically yield two solutions, known as roots, which can be found using various methods like factoring, completing the square, or using the quadratic formula.
Exploring Root Solutions
To find the roots of the equation 4x² + 5x + 12 = 0, one can apply the quadratic formula:
�=−�±�2−4��2�x=2a−b±b2−4ac
Where a, b, and c represent the coefficients of the quadratic equation. Substituting the values from 4x² + 5x + 12 = 0, we can compute the roots of x.
Unraveling Complexity
The nature of quadratic equations allows for real or complex roots. In this scenario, the discriminant (the value inside the square root of the quadratic formula) determines the nature of the sources. A positive discriminant yields two real roots, a zero discriminant results in repeated real roots, and a negative discriminant leads to complex roots.
Applications in Mathematics
Understanding quadratic equations and their solutions finds applications in various fields, from mathematics to physics and engineering. These equations model numerous natural phenomena, making them invaluable in solving real-world problems involving motion, trajectories, and more.
Bridging Mathematical Concepts
The 4x 2 5x 12 0 sequence bridges numerical lines and algebraic equations, showcasing how seemingly disparate numbers can encapsulate sophisticated mathematical concepts. Exploring such arrangements fosters a deeper appreciation for the interconnectedness of mathematical principles.
Embracing Mathematical Exploration
Mathematics is a tapestry of interconnected ideas and sequences like 4x 2 5x 12 0 offer glimpses into this intricate web. Embracing the curiosity to decipher these sequences sharpens analytical skills and nurtures a profound understanding of mathematical foundations.
Conclusion
In conclusion, the sequence 4x 2 5x 12 0, when interpreted as the quadratic equation 4x² + 5x + 12 = 0, provides a gateway to exploring the roots of quadratic equations and their applications in various domains. Embracing the exploration of numerical sequences fosters a deeper understanding of mathematical concepts and their real-world implications.
the sequence 4x 2 5x 12 0 provides a fascinating glimpse into numerical patterns, hinting at a quadratic equation 4x² + 5x + 12 = 0. Exploring such sequences not only sharpens mathematical reasoning but also reveals the beauty of numerical relations.